Thefashion2day Popular Fashion News Website
Related Articles
The logarithmic table is often used in math to discover the magnitude of any logarithmic equation. The log table is the easiest approach to get the magnitude of a particular logarithmic equation.
Once we supply everyone with a logarithm table through which you could obtain each of the numbers, before that, allow us to first define the logarithmic formula. An inverse of an exponential equation are the logarithmic functions. The following is the definition of a logarithmic equation:
For x, a > 0, and a≠1,
f(x) = x, if x =
f(x) is perhaps the Logarithmic equation to its base ‘a’ in this case. Base ‘e’ and base ’10’ have been the most often used bases in logarithmic operations.
Logarithm
The logarithm is actually the power whereby a base should always be increased in order to get a certain value. If = n, then x becomes the log of n towards the base b, something that is demonstrated arithmetically as x = n. For instance, = 81, therefore 4 is just the log of 81 to base 3, or 4 = 81. In that very similar way, because = 100, 2 = 100. Logarithms of the other type (such that trigonometric functions of bases 10) are referred to as common and thus are denoted by the symbol log n.
Types of Logarithms
- Standard Logarithm [f(x) = x]: The logarithmic function to base 10 (b = 10) is commonly referred to as the common logarithmic function, and it also has several uses in science as well as technology.
- Natural Logarithm [f(x) = x]: The natural log takes as its basis an integer e (2.718). As for it’s comparatively easy derivative, it is widely used in mathematics as well as physics.
Calculating Log of a Number
Rather than a simple computation, we may utilize the logarithmic table to get the log of an integer. While calculating the log of any number, one must first understand its characteristic as well as its mantissa parts.
- Characteristic Part – This component is just the entire collection of a number. A value higher than one has a positive feature, but if it is one less than that of total digits towards the left side of the decimal point in such a certain integer, it has a negative characteristic. When any integer is below one, the characteristic is minus, as well as the number is one higher than the amount of zeros towards the right side of it’s decimal point.
- Mantissa Part – This portion is the decimal portion of the log integer, which ought to be positive. If somehow the mantissa component has a negative number, it must be converted to a positive number. Visit Naa Songs to find out more information
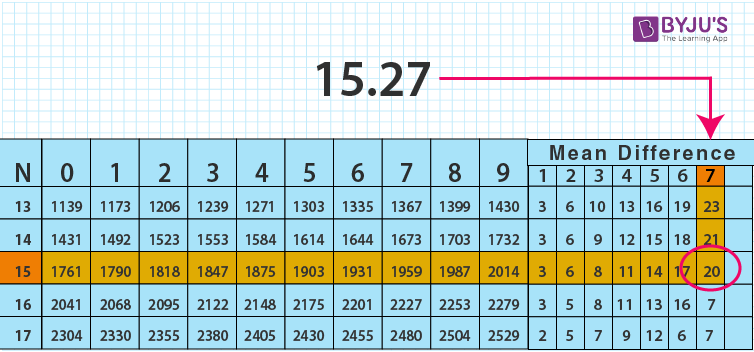
How to Use the Log Table?
- Step 1: Acknowledge a logarithmic idea. Every logarithmic table may only be used with a specific base. Log with base as ’10’ is often used as a form of a logarithmic chart.
- Step 2: Determine that number’s characteristic as well as the mantissa parts. To get the result of log10 (18.25), for instance, initially split the characteristic from the mantissa parts.
- Part of the Characteristic = 18
- Part of the mantissa = 25
- Step 3: Make use of a shared logarithm table. Then, utilize row 18 to verify column 2 then record its matching result. As a result, the outcome is 2601.
- Step 4: Measure the average differences using the log table. Move to its mean discrepancy column 5, row 18, and record the associated weight as 12.
- Step 5: Combine the values acquired in steps 3 & 4. This equals 2601 + 12 = 2613. As a result, the number 2613 represents this mantissa component.
- Step 6: Locate the distinguishing feature. Because this value lies between 10 & 100, the distinguishing feature must be 1.
- Step 7: At last, merge these two parts to get 1.2613.
